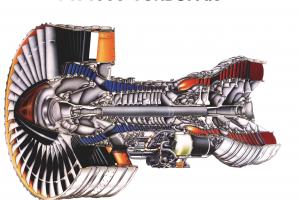
Jet Engine Research
In recent years a lot of attention has been devoted to the study of air flow through turbomachines. The main reason for this interest is that when a turbomachine, such as a jet engine, operates close to its optimal operating parameter values, the flow can become unstable. These instabilities put a large stress on the engine and in some cases the engine needs to be turned off in order to recover original operation. For this reason jet engines are currently operated away from their optimal operating parameter values increasing both fuel consumption and the engine weight.
Earthquake
The research develops a new mathematical theory of stochastic nonlinear partial differential equations to understand and advance the statistical theory of earthquakes. New models that give a better description of earthquake faults will be found and special solutions (solitons and breathers) that represent localized earthquakes propagating along the faults are studied. The mathematical seismology gives a firm foundation for the analysis of earthquake dynamics.
Erosion
The continuing evolution of the surface of the earth poses a challenging and fascinating modeling problem. The earth’s surface is composed of many substances: soil, sand, vegetation, different types of rocks. Its face is further complicated by topography which continues to change over time due to tectonic uplift and earthquakes. Due to the complexity of most landsurfaces and the instability of some it has taken many years to develop models.
Nanotechnology
The effective description of some quantum mechanical systems, far from a classical correspondence, can be nonlinear. Strongly driven THz intersubband transitions in AlGaAs/GaAs quantum wells are a good example of such a system and have been shown to exhibit novel nonlinear phenomena. Many-body effects which cause the nonlinearities become much more prominent in wide quantum wells (300 Angstrom) where intersubband spacing is of the order of 10 meV which is approximately that of the electron-electron Coulomb interactions.
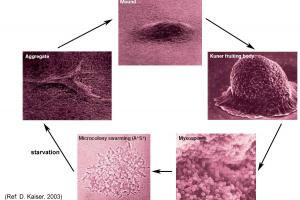
Mathematical Biology-Swarms of Bacteria
Myxobacteria (Myxococcus xanthus) change their life cycle according to food availability in their environment. In an ideal condition, myxobacteria grow as swarms that spread away from the center of a colony to search for nutrients from the medium and oxygen from above. However, when nutrients are depleted,myxobacteria undergo a phase transition in which they stop growing individually, but instead they merge and build a complex structure, called the fruiting body. The stage of fruiting body development is thus initiated by starvation and built by cell movements and interactions.
Mathematical Biology-Schools of Fish
Movements of living organisms have for centuries fascinated their observers. In recent year, much effort has been devoted to answer the question of what drives the complex behavior and patterns exhibited by organisms. Flocks of birds, swarms of locust, a cluster of bacteria and fish schools are examples of such.
Turbulence
The research goal is to develop new mathematical tools that open the theory of turbulence up to theoretical investigations. Great strides are currently being made both in turbulence experiments and simulations but the new mathematical development will allow theoreticians to compare with both simulations and experiments and make new predictions useful to both areas.